Circle Equation

All of you already know what circle is. But in mathematics, we define that a circle is the locus of all points equidistant to a point. Then the point is called, the central. And the distance is called radius. Mathematically, the equation of circle is very easy.

Equation of circle with central in the origin O(0,0) , and radius r.

Let T(x,y) in the circle. So, we have



Squaring both sides, we get



By this way, we get an equation of circle with central point in origin and radius r.

Equation of circle with central in the origin P(a,b) , and radius r.

Let T(x,y) in the circle. So, we have



by squaring both sides again, we get



So the equation of circle with the central point in P(a,b) and radius r is





Example.
Find the equation of circle which has radius 5 and the central point
a. in the origin
b. P(2,3)

Solution
a. By the equation above, we simply get



or

b. Analogue to the above, we get

Solving Linear Equation

"Linear" equations are equations with just a plain old variable like "x", rather than something more complicated like or or square roots or such. Linear equations are the simplest equations that you'll deal with. You've probably already solved linear equations; you just didn't know it.
In general, to solve an equation for a given variable, you need to "undo" whatever has been done to the variable. You do this in order to get the variable by itself; in technical terms, you are "isolating" the variable. This results in "(variable) equals (some number)", where (some number) is the answer they're looking for. For instance:
Solve

I want to get the x by itself; that is, I want to get "x" on one side of the "equals" sign, and some number on the other side. Since I want just x on the one side, this means that I don't like the "plus six" that's currently on the same side as the x. Since the 6 is added to the x, I need to subtract to get rid of it. That is, I will need to subtract a 6 from the x in order to "undo" having added a 6 to it. Here the mathematical way

Then the solution is -9

Go to the next example.

Solve



It's easy to solve it. Check it out





The idea is we add both sides by the same number, it is -5, then we get, y=-2. So the solution is y=-2.

Solving Quadratic Equations: Solving by Factoring

You should already know how to factor quadratics. The new thing here is that the quadratic is part of an equation, and you're told to solve for the values of x that make the equation true. Here's how it works:

Solve

Okay, this one is already factored for me. But how do I solve this?

Think: If I multiply two things to together and the result is zero, what can I say about those two things? I can say that at least one of them must also be zero. That is, the only way to multiply and get zero is to multiply by zero. (This is sometimes called "The Zero Factor Property" or "Rule" or "Principle".)

Warning: You cannot make this statement about any other number! You can only make the conclusion about the factors ("one of them must equal zero") if the product itself equals zero. If the above product of factors had been equal to, say, 4, then we would still have no idea what was the value of either of the factors; we would not have been able (we would not have been mathematically "justified") in making any claim about the values of the factors. Because you can only make the conclusion ("one of the factors must have equalled zero") if the product equals zero, you must always have the equation in the form "(quadratic) equals (zero)" before you can attempt to solve it.

The Zero Factor Principle tells me that at least one of the factors must be equal to zero. Since at least one of the factors must be zero, I'll set them each equal to zero:

x – 3 = 0 or x – 4 = 0

This gives me simple linear equations, and they're easy to solve:

x = 3 or x = 4

And this is the solution they're looking for:







Note that "x = 3, 4" means the same thing as "x = 3 or x = 4"; the only difference is the formatting. The "x = 3, 4" format is more-typically used.

---

One important issue should be mentioned at this point: Just as with linear equations, the solutions to quadratic equations may be verified by plugging them back into the original equation, and making sure that they work, that they result in a true statement. For the above example, we would do the following:

Checking x = 3 in (x – 3)(x – 4) = 0:

([3] – 3)([3] – 4) ?=? 0
(3 – 3)(3 – 4) ?=? 0
(0)(–1) ?=? 0
0 = 0

Checking x = 4 in (x – 3)(x – 4) = 0:

([4] – 3)([4] – 4) ?=? 0
(4 – 3)(4 – 4) ?=? 0
(1)(0) ?=? 0
0 = 0

So both solutions "check" and are thus verified as being correct.

---

solve

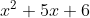
This equation is already in the form "(quadratic) equals (zero)" but, unlike the previous example, this isn't yet factored. The quadratic must first be factored, because it is only when you MULTIPLY and get zero that you can say anything about the factors and solutions. You can't conclude anything about the individual terms of the unfactored quadratic (like the 5x or the 6), because you can add lots of stuff that totals zero.

So the first thing I have to do is factor:

x² + 5x + 6 = (x + 2)(x + 3)

Set this equal to zero:

(x + 2)(x + 3) = 0

Solve each factor: Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

x + 2 = 0 or x + 3 = 0
x = –2 or x = – 3


The solution is -2 or -3

Checking x = –3 and x = –2 in x² + 5x + 6 = 0:

[–3]² + 5[–3] + 6 ?=? 0
9 – 15 + 6 ?=? 0
9 + 6 – 15 ?=? 0
15 – 15 ?=? 0
0 = 0

[–2]² + 5[–2] + 6 ?=? 0
4 – 10 + 6 ?=? 0
4 + 6 – 10 ?=? 0
10 – 10 ?=? 0
0 = 0

So both solutions "check".

Solve

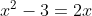
This equation is not in "(quadratic) equals (zero)" form, so I can't try to solve it yet. The first thing I need to do is get all the terms over on one side, with zero on the other side. Only then can I factor and solve:

x² – 3 = 2x
x² – 2x – 3 = 0
(x – 3)(x + 1) = 0
x – 3 = 0 or x + 1 = 0
x = 3 or x = –1

Then the solution to 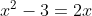is x=-1,3





Solve

• 

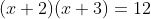
It is very common for students to see this type of problem, and say:

"Cool! It's already factored! So I'll set the factors equal to 12 and
solve to get x = 10 and x = 9. That was easy!"

Yeah, it was easy; it was also (warning!) wrong. Besides the fact that (10 + 2)(9 + 3) does not equal 12, you should never forget that you must have "(quadratic) equals (zero)" before you can solve.

So, tempting though it may be, I cannot set each of the factors above equal to the other side of the equation and "solve". Instead, I first have to multiply out and simplify the left-hand side, then subtract the 12 over to the left-hand side, and re-factor. Only then can I solve.

(x + 2)(x + 3) = 12
x² + 5x + 6 = 12
x² + 5x – 6 = 0
(x + 6)(x – 1) = 0
x + 6 = 0 or x – 1 = 0
x = –6 or x = 1


Then the solution is x=-6, 1




Solve

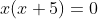
A very common mistake that students make on this type of problem is to "solve" the equation for "x + 5 = 0" by dividing off the x. But you can't divide by zero; dividing off the x makes the implicit assumption that x is not zero. There is no justification for making that assumption! And (warning!) making that (implicit) assumption will cause you to lose half of your solution to this problem.

Even though you are used to variable factors having variables and numbers (like the other factor, x + 5), a factor can contain only a variable, so "x" is a perfectly valid factor. So set the factors equal to zero, and solve:

x(x + 5) = 0
x = 0 or x + 5 = 0
x = 0 or x = –5


then the solution is x=0, -5

Reflection of the Video

Video I

Video II

Video III

Video IV



Video V

Multiple Integral: Definition

Lec 3 | MIT 18.02 Multivariable Calculus

Lec 2 | MIT 18.02 Multivariable Calculus

Cindy is riding on an elevator in a building that has many
floors and one basement floor underground. Answer these
questions regarding Cindy's adventure riding the elevator up and
down the building.

1) From the first floor, Cindy goes up 8 floors and then down
3 floors. What floor is she now on?
2) Cindy is on the 18th floor. She goes down 10 floors and then
up 13 floors. What floor is she now on?
3) Cindy is on the 7th floor. She then goes up to the 19th floor.
How many floors did she go up?
4) Cindy is on the 2nd floor. She goes down 3 floors. What floor
is she now on?
5) From the top floor, Cindy goes down to the 8th floor,
travelling 17 floors. What is the top floor?
6) Cindy does not know what floor she is on. She presses the
button to go to the 10th floor and the elevator travels 4
floors. What floor was she on originally?

Multivariabel Calculus, Lecture 1, MIT

this is lecture 1 in Multivariable Calculus in MIT

LET ME COUNT THE WAYS

1) Tina has 3 shirts-red, blue, and yellow. She also has 2 skirts-
black and white. Each day, she wears a different shirt with a
different skirt.

A) For how many days can she do this before she must repeat and

Draw pictures of Tina and color if you wish.

There is also a chart called a TREE that can help Tina to know
which outfit is next to wear. It looks like this:

|-----Black
|---Red-------|
| |-----White
|
|
| |-----Black
|--Blue-------|
| |-----White
|
|
| |-----Black
|--Yellow-----|
|-----White

So, you can see all the possibilities and even count them.

C) Uh oh, Tina accidentally ripped her yellow shirt and cannot wear
it anymore. How many outfits does she have now? Draw a tree.

2) When Billy comes home from school each day, he gets a snack
and a drink. His Mom lets him choose either a piece of fruit, a
cookie, or a peanut butter sandwich. He can drink juice,
milk, or a soda.

A) Can you make a TREE that explains all the possibilities of
snacks and sodas? How many snack and drink combinations are there?

B) How many combination are there if the drink is MILK?

The Meaning of Mathematics

When we talk about mathematics, what should we know about it? Is Mathematics about “monster” as many people (who don’t like it) say? Or about mystery for the one who like it?
Many question come from our mind to know and to understand about mathematics. But the answer can be found by reflecting what the really mean of mathematics is. Actually we will not be able to live without mathematics. Everything around us are depend on mathematics.
Mathematics is very useful both in our daily life and in the developing other sciences. Mathematics is science of truth and the body of science. Physics needs mathematics to solve the problem. Chemistry, Biology and other sciences is supported by the useful mathematics.
We can see the mathematics as a science. As a science, Mathematics has objects. The object of mathematics is the material object and formal object. Mathematics material objects are in our minds. We can only imagine the object of mathematics in our minds, because the object of mathematics is abstract, different with the other sciences which is usually the material object is the concrete object as in our daily life.
During this time people think that the material object of mathematics is a numeral. Actually it does not matter if they think like that. However, it needs to straighten the true meaning of mathematics. The numeral is only a symbol to represent a number. Until this time, something what called "seven", we always represents with 7. So in fact we speak about the value of the number of seven, not the numeral of seven. Once again, the symbol is only one way to show us that we think about number seven. We can give another symbol for the number seven.
Actually there are many different symbols to indicate a number. There are Roman numerals, Babylonia numerals, and so forth. Even the numerals have emerged in the very long time. So, essentially if we talk about mathematics, we talk about the values and the characteristics of the objects of mathematics.
The formal object Mathematics is a way of approach to the mathematics material objects. Here, there are many ways of approach in mathematics. As was mentioned above that the Mathematics looks at the characteristics and the value of the object.
Mathematics looks at its object deductively, it means that Mathematics look it in general. For example if we are talking about set, then the attributes attached to the set that must also be attached to the element of the set, otherwise it is not element of the set.
That's a little story about Mathematics, hopefully we can add insight to what is called Mathematics.