You should already know how to factor quadratics. The new thing here is that the quadratic is part of an equation, and you're told to solve for the values of x that make the equation true. Here's how it works:
Solve

Okay, this one is already factored for me. But how do I solve this?
Think: If I multiply two things to together and the result is zero, what can I say about those two things? I can say that at least one of them must also be zero. That is, the only way to multiply and get zero is to multiply by zero. (This is sometimes called "The Zero Factor Property" or "Rule" or "Principle".)
Warning: You cannot make this statement about any other number! You can only make the conclusion about the factors ("one of them must equal zero") if the product itself equals zero. If the above product of factors had been equal to, say, 4, then we would still have no idea what was the value of either of the factors; we would not have been able (we would not have been mathematically "justified") in making any claim about the values of the factors. Because you can only make the conclusion ("one of the factors must have equalled zero") if the product equals zero, you must always have the equation in the form "(quadratic) equals (zero)" before you can attempt to solve it.
The Zero Factor Principle tells me that at least one of the factors must be equal to zero. Since at least one of the factors must be zero, I'll set them each equal to zero:
This gives me simple linear equations, and they're easy to solve:
And this is the solution they're looking for:

Note that "x = 3, 4" means the same thing as "x = 3 or x = 4"; the only difference is the formatting. The "x = 3, 4" format is more-typically used.
One important issue should be mentioned at this point: Just as with linear equations, the solutions to quadratic equations may be verified by plugging them back into the original equation, and making sure that they work, that they result in a true statement. For the above example, we would do the following:
Checking x = 3 in (x – 3)(x – 4) = 0:
Checking x = 4 in (x – 3)(x – 4) = 0:
So both solutions "check" and are thus verified as being correct.
solve
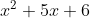
This equation is already in the form "(quadratic) equals (zero)" but, unlike the previous example, this isn't yet factored. The quadratic must first be factored, because it is only when you MULTIPLY and get zero that you can say anything about the factors and solutions. You can't conclude anything about the individual terms of the unfactored quadratic (like the 5x or the 6), because you can add lots of stuff that totals zero.
So the first thing I have to do is factor:
Set this equal to zero:
Solve each factor: Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved
Checking x = –3 and x = –2 in x2 + 5x + 6 = 0:
So both solutions "check".
Solve
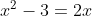
This equation is not in "(quadratic) equals (zero)" form, so I can't try to solve it yet. The first thing I need to do is get all the terms over on one side, with zero on the other side. Only then can I factor and solve:
x2 – 3 = 2x
x2 – 2x – 3 = 0
(x – 3)(x + 1) = 0
x – 3 = 0 or x + 1 = 0
x = 3 or x = –1
Then the solution to 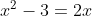 is x=-1,3
is x=-1,3
Solve
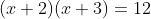
It is very common for students to see this type of problem, and say:
"Cool! It's already factored! So I'll set the factors equal to 12 and
solve to get x = 10 and x = 9. That was easy!"
Yeah, it was easy; it was also (warning!) wrong. Besides the fact that (10 + 2)(9 + 3) does not equal 12, you should never forget that you must have "(quadratic) equals (zero)" before you can solve.
So, tempting though it may be, I cannot set each of the factors above equal to the other side of the equation and "solve". Instead, I first have to multiply out and simplify the left-hand side, then subtract the 12 over to the left-hand side, and re-factor. Only then can I solve.
(x + 2)(x + 3) = 12
x2 + 5x + 6 = 12
x2 + 5x – 6 = 0
(x + 6)(x – 1) = 0
x + 6 = 0 or x – 1 = 0
x = –6 or x = 1
Then the solution is x=-6, 1
Solve
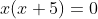
A very common mistake that students make on this type of problem is to "solve" the equation for "x + 5 = 0" by dividing off the x. But you can't divide by zero; dividing off the x makes the implicit assumption that x is not zero. There is no justification for making that assumption! And (warning!) making that (implicit) assumption will cause you to lose half of your solution to this problem.
Even though you are used to variable factors having variables and numbers (like the other factor, x + 5), a factor can contain only a variable, so "x" is a perfectly valid factor. So set the factors equal to zero, and solve:
x(x + 5) = 0
x = 0 or x + 5 = 0
x = 0 or x = –5
then the solution is x=0, -5



